
ここに最高気温とアイスティーの売上げを列記したデータがある。これについて回帰分析を行う。
最高気温を材料にしてアイスティーの売上げを推定できるか調べる。 このような推定を専門的表現で「アイスティーの売上げを最高気温に回帰させる」というらしい。
まず、回帰分析を行う意味のあるデータなのかどうかを確認する。
2つの項目の相関が認められなければ、 回帰分析の結果が実質的な意味を持たない。
「最高気温」と「アイスティーの売上げ」の相関係数を確認すると次のとおり。
r=0.906923, df=12, p-value=7.66141e-06
有意な強い相関が認められる。
ちなみに、散布図は図1のようになる。

強い相関が認められるので、回帰分析を行ってみた。その結果は次のとおり。
つまり、次のような推定のための計算式(回帰式)が求められる。
「アイスティーの売上げ」=-36.36123+3.737885×「最高気温」
上の回帰式によって描かれる直線が回帰直線である。
散布図に回帰直線を書き入れてみると図2のようになる。
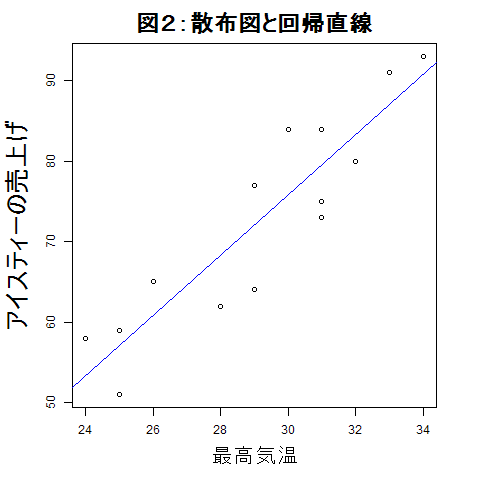
個々の実測値と回帰式から得られる値との間には誤差(残差)がある。 すべての実測値についてこの誤差の平方和が最小になるように 考え出されたのが上の回帰式である。
先の回帰式がどの程度信頼できるかをみる一つの手がかりは、決定係数である。
決定係数は、1に近いほど信頼性が高い。
今回の 0.8225093 という値は、「アイスティーの売上げ」の変動が「最高気温」の変動によって 82.3%だけ説明できることを意味している。
残りの17.7%は、回帰式に含まれていない別の要素が関係しているとみられる。
決定係数の信頼性はF検定の結果により判断する。もっともっと幅広く 調査したとき、もしかすると決定係数が0になるかもしれない。その危険性を 示すのがF検定のp値である。これが0.05(5%)とか0.01、あるいは0.001より 小さければ、そのレベルに応じた有意性が認められることになる。
このp値が0.05以上だと、「母集団において決定係数が0である」 という仮説を、母集団に関して棄却できないことになる。
回帰係数(coefficient:y切片やxの傾きの関連) に関する詳細な情報を掲げると次のとおり。
| 見積り | 標準誤差 | t検定値 | t検定時のp値 | |
|---|---|---|---|---|
| 定数項 | -36.3612334801762 | 14.6872670894724 | -2.47569770867988 | 0.0291872649368303 |
| 最高気温 | 3.73788546255507 | 0.501248142954886 | 7.45715573232854 | 7.66141280445013e-06 |
この表で、1行目の「定数項」の「見積り」はy切片の値であり、 2行目の「最高気温」の「見積り」の欄はxの傾きの値である。
重回帰分析の場合は、説明変数の個数に応じて、 3行目・4行目・……が表示されることになる。
表の右端の「t検定時のp値」は、該当の変数が実は影響力を 持たないかもしれない危険性(確率)を示す。
xの傾きが0であれば、xの値が何であってもyの値に影響しない。
最高気温の傾きが3.737885と見積もられてはいるが、もっともっと調査対象を拡げると、 実は0ということもあるかもしれない。その「かもしれない」の確率がp値である。 p値が十分小さければ、有意性が認められることになる。
定数項のp値については、実際に言及することは少ないと思うが、 もっともっと幅広く調査した時にy切片が0であるかもしれない確率を示す。