ここに「重症度, 総コレステロール, 中性脂肪」を列記したデータがある(N=10)。 これについて回帰分析を試みる。
「総コレステロール, 中性脂肪」を材料にして「重症度」を推定できるか調べる。
| 患者No. | 総コレステロール | 中性脂肪 | 重症度 |
|---|---|---|---|
| 1 | 220 | 110 | 0 |
| 2 | 230 | 150 | 1 |
| 3 | 240 | 150 | 2 |
| 4 | 240 | 250 | 1 |
| 5 | 250 | 200 | 3 |
| 6 | 260 | 150 | 3 |
| 7 | 260 | 250 | 2 |
| 8 | 260 | 290 | 1 |
| 9 | 270 | 250 | 4 |
| 10 | 280 | 290 | 4 |
まず、「重症度, 総コレステロール, 中性脂肪」の各要素の組みについて相関係数を算出する。
それを表形式で示すと次のとおり。
| 重症度 | 総コレステロール | 中性脂肪 | |
|---|---|---|---|
| 重症度 | 1 | 0.827 | 0.386 |
| 総コレステロール | 0.827 | 1 | 0.753 |
| 中性脂肪 | 0.386 | 0.753 | 1 |
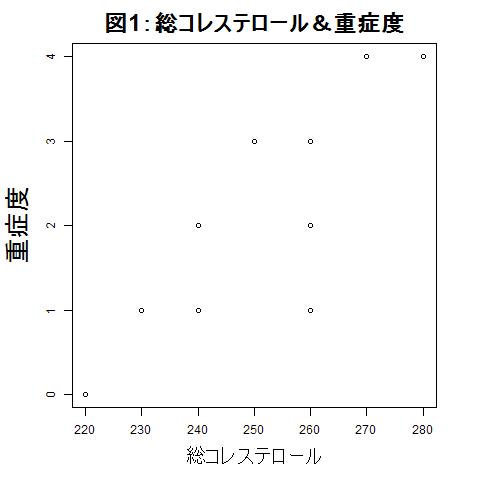
目的変数と各説明変数の組みに関する散布図は図1〜図2のようになる。


回帰分析を行った結果、次のような推定のための計算式(回帰式)が求められた。
「重症度」 = -18.5014 + 0.09162236 × 「総コレステロール」 + -0.01146323 × 「中性脂肪」
次に決定係数関連の情報を列記する。
| 決定係数 | 0.8137019 |
| 自由度調整済み決定係数 | 0.7604739 |
| F検定の値 | 15.28709(df: 2 〓 7) |
| F検定のp値 | 0.002790805 |
今回の決定係数 0.8137019 という値は、「重症度」の変動が「総コレステロール, 中性脂肪」の変動によって 81.4%だけ説明できることを意味している。
残りの18.6%は、回帰式に含まれていない別の要素が関係しているとみられる。
決定係数の信頼性はF検定の結果により判断する。もっともっと幅広く 調査したとき、もしかすると決定係数が0になるかもしれない。その危険性を 示すのがF検定のp値である。これが0.05(5%)とか0.01、あるいは0.001より 小さければ、そのレベルに応じた有意性が認められることになる。
このp値が0.05以上だと、「母集団において決定係数が0である」 という仮説を、母集団に関して棄却できないと判断する。
回帰係数(coefficient:y切片や偏回帰係数)についての情報を 掲げると次のとおり。
| 見積り | 標準誤差 | t検定値 | t検定時のp値 | |
|---|---|---|---|---|
| 定数項 | -18.5013972443237 | 3.85620225141615 | -4.7978285468635 | 0.00197122423421542 |
| 総コレステロール | 0.0916223559091791 | 0.0183291541405596 | 4.99872253823393 | 0.00156753202654268 |
| 中性脂肪 | -0.0114632253056472 | 0.00519335137833611 | -2.2072886023976 | 0.0630490540761245 |
この表で、1行目の「定数項」の「見積り」はy切片の値であり、 2行目の「総コレステロール」の「見積り」の欄は 当該説明変数の偏回帰係数の値である。
表の右端の「t検定時のp値」は、該当の変数が実は影響力を 持たないかもしれない危険性(確率)を示す。
偏回帰係数が0であれば、該当の説明変数の値が何であっても 目的変数の値に影響を与えない。
「総コレステロール」の係数が0.09162236と見積もられてはいるが、 もっともっと調査対象を拡げると、実は0ということもあるかもしれない。 その「かもしれない」の確率がp値である。 p値が十分小さければ、有意性が認められることになる。
定数項のp値については、レポートなどで言及することは少ないと思うが、 もっともっと幅広く調査した時にy切片が0であるかもしれない確率を示す。
参考まで、残差(誤差)および目的変数の実測値の2つについて、 その分布に関する主な数値を掲げる。 残差は、回帰式の値(予測値)と実測値との差。
| Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. | |
|---|---|---|---|---|---|---|
| 残差 | -0.9961 | -0.4396 | 0.1596 | -5.559e-18 | 0.3413 | 0.8885 |
| 重症度 | 0 | 1 | 2 | 2.1 | 3 | 4 |
今回の重回帰分析は、下のサイトを参考にさせていただきました。 素材データも、そこに掲げられているものです。
上のサイトでは、統計的な値の算出方法をはじめ、 いろいろな事柄について丁寧に解説されています。 重回帰分析に限らず、様々な分析についての解説があります。
オリジナルの表にあったTC, TGは、私にはイメージしにくい用語だったので
TC:総コレステロール、TG:中性脂肪
と変更した上で統計処理を行っています。
当該webを出力するためのrubyスクリプトは
lm_m.rb です。
回帰分析の簡単なレポート作成
で紹介しているrubyスクリプトを重回帰分析用に書き換えました。
ruby lm_m.rb [enter]
上のように実行すると lm_m.htm が書き出されます。 それをブラウザで開くと、当該webと同じ内容になっているはずです。
用いているruby用ライブラリは次のとおり。 括弧内は私のところでインストールしてあるバージョンの番号です。
なお、webから素材データをちゃんと取得できたかを後で確認できるよう、 src_data.csv を書き出すようにしました。これには、統計の素材としたテーブルと、 webにあったオリジナルのテーブルの2つが含まれています。
また、markdownの原稿をmkd_m.txt というファイルに書き出すようにしました。 これをkramdownでhtmlに変換したのが当該webです。
〜 以上 〜